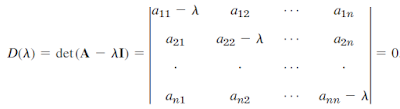The process of finding an unknown scalar, λ and a nonzero vector, x for a given non zero square matrix, A of dimension n x n is called matrix eigenvalue or eigenvalue.
Ax = λ x
The λ and x which satisfies the above equation is called eigen value and eigenvector.
Ax should be proportional to x. The multiplication will produce a new vector that will have the same or opposite direction as the original vector.
The set of all the eigenvalues of A is called the spectrum of A. The largest of the absolute values of the eigenvalues of A is called the spectral radius of A.
To determine eigenvalue and eigenvector,
the equation can be written in matrix notation,
(A - λI)x = 0
By Cramer's theorem, the homogeneous linear system of equations has a nontrivial solution if and only if the corresponding determinant of the coefficients is zero.
A - λI is called characteristic matrix and D(λ) is characteristic determinant of A. The above equation is called characteristic equation of A.
The eigenvalues of a square matrix A are the roots of the characteristic equation of A.
Hence an n x n matrix has at least one eigenvalue and at most n numerically different eigenvalues.
The eigenvalues must be determined first and its corresponding eigenvectors are obtained from the system.
The sum of the eigenvalues of A equals the sum of the entries on the main diagonal of A, called the trace of A.
