Skip to main content

Tree Data Structure

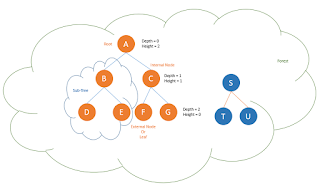
A tree is an abstract model of a hierarchical structure. The tree consists of nodes with a parent-child relation. The each element of the tree except the top element, has a parent and zero or more children elements.
The few applications of tree structure are Organization Data, Compiler processing, File system, Searching algorithm etc.
The node without parent is called Root.
The nodes with at least one child is called Internal nodes.
The nodes without children is called External nodes or Leaf.
The nodes which share the same parent is called Siblings.
The parent, grandparent, great-grandparent of a node is called Ancestor.
The child, grandchild, great-grandchild of a node is called Descendant.
The number of children of a node is called Degree.
The number of edges in path from root node to a node is called Depth of the node.
The number of edges in longest path from a node to a leaf is called Height of the node.
A node and its descendants in a tree is called Sub-tree.
The level of a tree is set of all nodes at the same depth. The level of Root is 0.
The set of disjoint trees are called Forest.
Labels:

Popular posts from this blog

Exercise 2 - Amdahl's Law

A programmer has parallelized 99% of a program, but there is no value in increasing the problem size, i.e., the program will always be run with the same problem size regardless of the number of processors or cores used. What is the expected speedup on 20 processors? Solution As per Amdahl's law, the speedup,  N - No of processors = 20 f - % of parallel operation = 99% = 1 / (1 - 0.99) + (0.99 / 20) = 1 / 0.01 + (0.99 / 20) = 16.807 The expected speedup on 20 processors is 16.807
Read more

Exercise 1 - Amdahl's Law

A programmer is given the job to write a program on a computer with processor having speedup factor 3.8 on 4 processors. He makes it 95% parallel and goes home dreaming of a big pay raise. Using Amdahl’s law, and assuming the problem size is the same as the serial version, and ignoring communication costs, what is the speedup factor that the programmer will get? Solution Speedup formula as per Amdahl's Law, N - no of processor = 4 f - % of parallel operation = 95% Speedup = 1 / (1 - 0.95) + (0.95/4) = 1 / 0.5 + (0.95/4) Speedup = 3.478 The programmer gets  3.478 as t he speedup factor.
Read more

Minor, Cofactor, Determinant, Adjoint & Inverse of a Matrix

Consider a matrix Minor of a Matrix I n the above matrix A, the minor of first element a 11  shall be Cofactor The Cofactor C ij  of an element a ij shall be When the sum of row number and column number is even, then Cofactor shall be positive, and for odd, Cofactor shall be negative. The determinant of an n x n matrix can be defined as the sum of multiplication of the first row element and their respective cofactors. Example, For a 2 x 2 matrix Cofactor C 11 = m 11 = | a 22 | = a 22  = 2 Determinant The determinant of A is  |A| = (3 x 2) - (1 x 1) = 5 Adjoint or Adjucate The Adjoint matrix of A , adjA is the transpose of its cofactor matrix. Inverse Matrix A matrix should be square matrix to have an inverse matrix and also its determinant should not be zero. The multiplication of matrix and its inverse shall be Identity matrix. The square matrix has no inverse is called Singular. Inv A = adjA / |A|           [ adjoint A / determ...
Read more